Training neural networks can drain the world of all power
A new paper proves that training neural networks is even harder. All the world's energy can be used to train a single network of modest size without reaching the optimum. This calls for restricting the training process and clever ways to replace the use of neural networks.
Assistant professor and BARC member Mikkel Abrahamsen explains the result of his paper Training Neural Networks is ∃ℝ-complete written together with Linda Kleist and Tillmann Miltzow. The paper was recently accepted at the prestigious conference NeurIPS (Advances in Neural Information Processing Systems 2021) and can be found here: https://arxiv.org/abs/2102.09798
A neural network is a brain-inspired machine learning model that can be trained to perform complex and diverse tasks at super-human level. Neural networks have time and again shown to be superior to all other known techniques for problems such as playing difficult games like chess and go, translating languages, recognizing human faces, identifying cancer in CT scans, etc. Neural networks are extensively used in social media to model the behaviour of users. These models are used to customize the content seen by a user, such as advertisements.
Before a neural network is of any use, it must be trained on known examples, such as a large collection of CT scans where a human expert has pointed out which scans show signs of cancer and which do not. The neural network then learns the pattern and can spot cancer in new unseen scans. Once the training is done, it is fast and efficient to use the network over and over again, but unlimited amounts of energy and time can be used on the training itself.
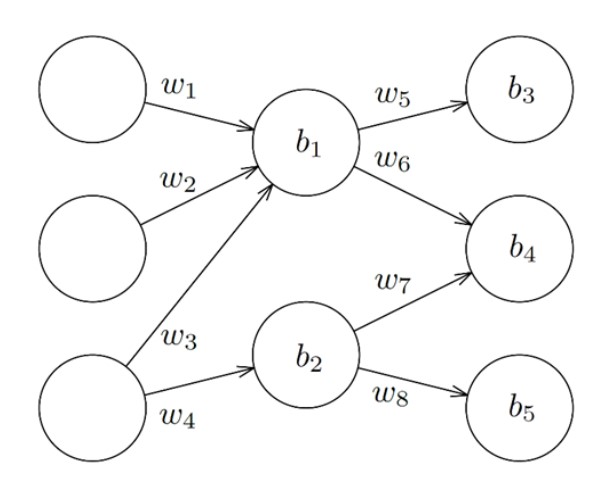
The figure shows a simple example of a neural network. Numbers are fed into the three nodes to the left. The numbers flow through the network and are multiplied by the weights (the w’s) and the biases are added (the b’s). Training the network means to choose the parameters (the weights and the biases) so that the results produced by the network match those known from training data.
The new paper shows that the problem of training a neural network to the optimal stage is complete for a complexity class known under the peculiar name ∃ℝ, or the Existential Theory of the Reals. This means that the problem is essentially as hard as solving some very general equations with many unknowns; a problem for which only horribly slow algorithms are known. In practice, equations with at most eight unknowns can be handled within reasonable time, while neural networks can have billions of parameters that must be chosen during training. Even quantum computers are not expected to be able to solve these kinds of hard problems.
In a world where neural networks play an increasingly prominent role, the paper fills an important gap in our knowledge. Vast amounts of energy is currently being used to train neural networks, so understanding the complexity of the training problem is crucial. Using the methods from the paper, it is straightforward to construct a neural network of modest size that is particularly tricky to train: With the algorithms currently known, one may easily use the world's entire production of energy for many years without reaching the optimum.
While neural networks can be used in many ways that improve the wellbeing of people, the result underlines the importance of only using the networks where it is necessary. Likewise, we must accept that the training process cannot be completed, but must be stopped before reaching the optimal stage. Unlimited resources can be used to improve a network, and the question is how long it is responsible to proceed.
Neural networks are usually trained using variants of an algorithm called backpropagation. Simply speaking, the algorithm adjusts the parameters (the weights and biases) of the network little by little to match the training data better and better. There exist many other methods for optimization that appear much more sophisticated, but they have so far been of no use in training neural networks. The paper gives an explanation why, namely that these other methods are tailored for problems in a complexity class known as NP, which is believed to be smaller and easier than ∃ℝ.
Subsequent work will focus on building a bridge between neural networks and other problems known to have the same complexity. For instance, the backpropagation algorithm, which has been fine-tuned to train neural networks using specialized hardware, may turn out useful for packing objects in the most space-efficient way, as such packing problems have likewise been shown to be ∃ℝ-complete. Another research direction is to further explore the consequences of the high complexity and determine exactly what features cause the neural networks to be that hard to train.
