Researchers determine the difficulty of cutting Christmas cookies optimally
BARC recently got four papers accepted for the conference FOCS 2020 (the 61st Annual IEEE Symposium on Foundation on Computer Science), which is considered the most prestigious of all conferences in theoretical computer science.
Assistant professor Mikkel Abrahamsen here explains the result of his paper Framework for ∃R-Completeness of Two-Dimensional Packing Problems written together with Tillmann Miltzow and Nadja Seiferth. The paper can be found here.
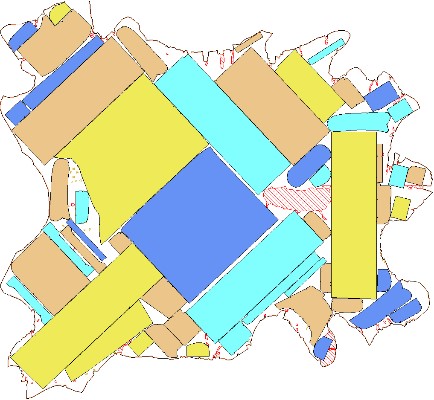
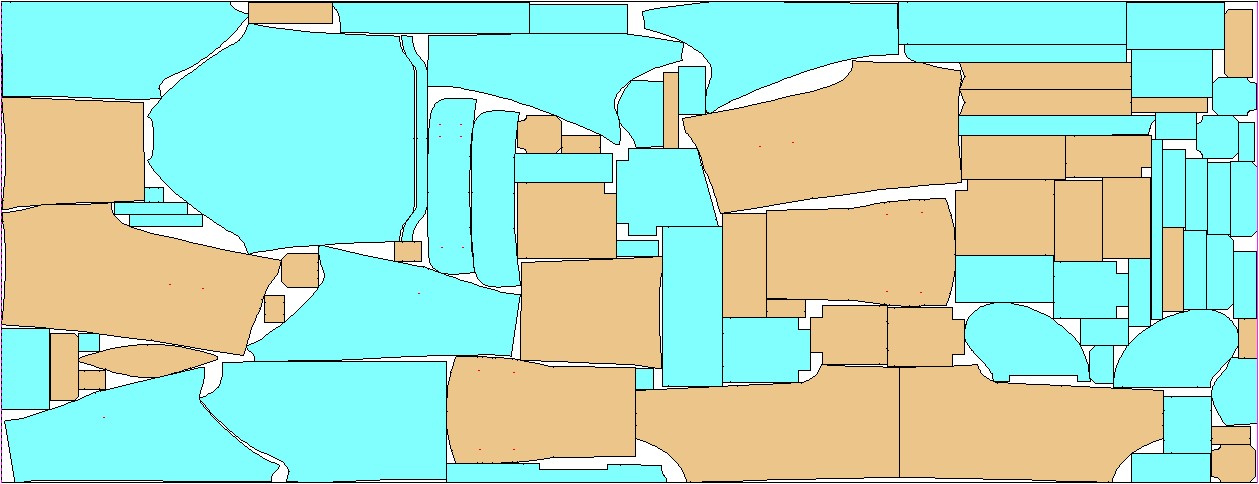
Figure 1. Real examples of nesting on a leather hide (top) and a piece of fabric (bottom), kindly provided by MIRISYS and produced by their software for automatic nesting, https: //www.mirisys.com/.
The result of the paper is a determination of how hard it is to solve many versions of 2D packing problems. In a packing problem, one has a container and a set of pieces, and the goal is to find a way to place the pieces in the container such that they do not overlap, or to determine that there is not enough space in the container to do so. Such problems occur everywhere in our daily lives. To give a few examples, you solve packing problems when you choose where to place your furniture, the manufacturer of your clothing arranges cutting patterns on a large piece of fabric in order to minimize waste, and at Christmas time, you are trying to cut out as many cookies from a dough as you can.
In a large number of industries, it is crucial to solve complicated instances of packing problems efficiently. In addition to clothing manufacturing, we mention leather, glass, wood, and sheet metal cutting, selective laser sintering, shipping (packing goods in containers), and 3D printing (arranging the parts to be printed in the printing volume); see Figure 1.
Different applications lead to different packing problems. For instance, when arranging cutting patterns on a roll of fabric for clothing production, the orientation of each piece has to follow the orientation of the weaving or a pattern printed on the fabric, so here, the pieces should not be rotated. In other contexts such as leather, glass, or sheet metal cutting, there are usually no such restrictions, so rotations can be used to minimize waste. Other versions arise when the shape of the container or the pieces is restricted.
Most versions of packing problems were already known to be NP-hard. In the paper, we show that many are likely to be even harder by proving them to be ∃R-complete. This includes the problem of packing polygons into a square with rotations allowed. The result means that these problems are essentially as hard as deciding if a system of polynomial equations and inequalities has a real solution – a problem expected by most researchers to be more difficult than the NP-complete problems, although this remains an outstanding open question in the field. Please keep this in mind the next time you are cutting out Christmas cookies!
