Reconstructing The Evolutionary Tree of Life with BARC

Reconstructing The Tree of Life with BARC

How can one trace the history of evolution? Is it possible to reconstruct the tree of life, despite our limited knowledge of the past? When we are lucky, fossils and similar findings may guide us. In general, however, we are left with understanding evolution by only observing today’s species.

As an (oversimplified) example, consider the following reasoning: humans and monkeys look quite similar. Much more similar than any of them look to an elephant. Maybe they both had a common ancestor in the near past, but the elephant does not descend from this ancestor. Such ancestor-descendant relationships form an evolutionary tree, or the tree of life as Charles Darwin called it.

Why should we care about this tree though? It turns out that an evolutionary tree inducing a hierarchical classification of species is not just tied to biology. Medicine, ecology and linguistics are just some of the fields where this concept appears, and it is even an integral part of machine learning and data science. In fact, discussions related to the reconstruction of the optimal such tree are traced back to Plato and Aristotle (350 BC).

An illustration is given below for four species. On the left, we have a distance matrix describing the dissimilarity between species, and on the right, we have a corresponding evolutionary tree, or phylogeny.

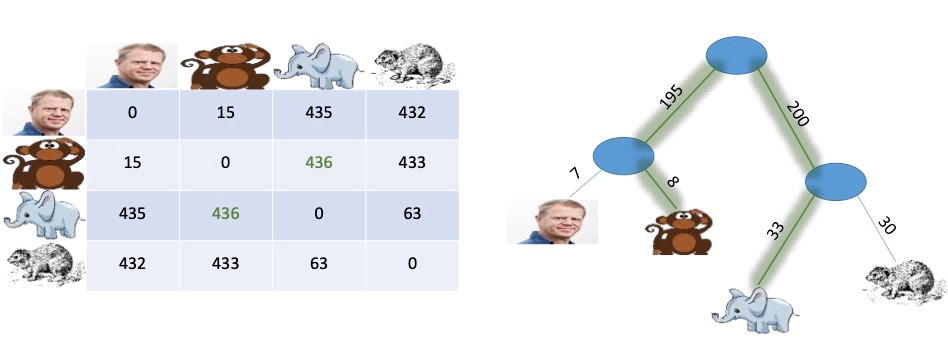
We have added weights to the edges in the tree so that when we sum the weights on the path between two species, we get their distance, e.g., the distance between the monkey and the elephant is 8+195+200+33=436.

In the above example, there is an exact match between the distances in the matrix and the distances in the tree, and in such cases, it is easy for a computer to construct the evolutionary tree matching a given distance matrix. This has been known since 1977.

However, reality is not perfect. Measured distances may have noise and evolution is not quite so simple, and typically there will be no evolutionary tree matching a given measured distance matrix, e.g., if the distance between the monkey and the elephant was measured as 450 and the other distances were the same, then our current evolutionary tree would still offer the best approximation, even though it makes an error of |450-436|=14 on one of the distances.

We now have to explain what we mean by a best match between a distance matrix and an evolutionary tree when there is no perfect tree. A classic measure is the total error, that is, the sum of errors over all pairs of species. The evolutionary tree minimizing the total error relative to a measured distance matrix is then seen as a best guess for the underlying evolutionary tree. Finding such a tree is a very challenging problem when there is no exact match. In Science this is an instance of the Numerical Taxonomy Problem, which has a rich literature. There are many methods producing an evolutionary tree from a distance matrix, but typically, we have no idea if any of them are even close to the best possible.

Let us try to appreciate the difference between a good and a best match. Think of trying to get to the highest point on planet earth with no global understanding of where it is; namely, the top of Mount Everest. A simple idea is that a bunch of climbers each go to a random place and then, locally, climb as high as possible. Surely some of them must get very high, but if none of them start at the Tibetan plateau, then none of them will get close to the highest point. Indeed, this illustrates the issue with many best-effort heuristics.

Returning to our concrete problem, for a given distance matrix, we may try a lot of different trees, and see if we can locally improve on the weights and the internal structure to better match the distance matrix (the local improvements correspond to climbing to the highest local peak), but there is no guarantee that we will get even close to the best match. This is a problem because the whole idea is that there is an underlying evolution and that the corresponding evolutionary tree, despite noise, should be a very good match for the measured distances. Our goal is to find a similarly strong match, that is, a tree with a guarantee that its match is not too much worse than the best possible. More formally, we want a tree that minimizes the total error, at least within a constant factor. However, deciding if there exists an efficient algorithm that can always minimize the total error within a constant factor has evolved over the last 30 years as big challenge within theoretical computer science.

Recently, a group of three researchers from BARC-UCPH (Debarati Das, Evangelos Kipouridis, Mikkel Thorup) and two former UCPH researchers now working at Google Research (Vincent Cohen-Addad, Nikos Parotsidis) resolved this old challenge. They presented an efficient algorithm that for any distance matrix is guaranteed to find an evolutionary tree minimizing the total error within an absolute constant factor, that is, a factor which is independent of the number of species involved.

"Back at 1995 I was working with a similar problem, namely that of finding a tree minimizing the maximum error. Even though minimizing the total error was a more natural target, the guarantees of our solution were so much stronger that eventually our algorithm ended up being used by biologists all over the world. After all, the whole community, me included, believed that strong guarantees were impossible to achieve for the more natural total-error version", says Professor Thorup. "However, in 2019, after almost 25 years, we observed some underlying structure that gave us hope of similarly strong guarantees for the total error".

 

The perspective of Theoretical Computer Science.

Mathematically speaking, we want algorithms that are efficient in the sense that the running time is polynomial in the input size, and with quality guarantees that hold for any possible input. In this case, the ideal guarantee would be to output a tree metric with the smallest possible total error relative to the input distance matrix. However, in 1987, this was proved to be NP-hard. NP-hard means that it is impossible to do in polynomial time assuming NP≠P. This assumption is widely believed to be true, but proving it is one of the biggest challenges in mathematics and one of the seven Millennium Prize Problems.

Since getting an optimal solution is NP-hard, one should settle for a so-called approximation factor A such that if for any given distance matrix, the nearest tree metric has a total error of X then the algorithm should be guaranteed to find a tree whose total error is at most A*X. Such a mathematical guarantee for all inputs is very different from the approach of best-effort heuristics that are compared experimentally, testing which one does best on some concrete benchmarks with no knowledge of what is the optimal solution for these benchmarks, and no guarantee for how the heuristics will perform on other inputs.

The new algorithm's approximation factor is an absolute constant, and an absolute constant is the best possible assuming NP≠P. All previous solutions had a super constant approximation factor that grew with the number n of species. The previous best factor dates back to 2005 and was proportional to (log n)(log log n) by Ailon and Charikar. Charikar is the world star within approximation algorithms and clustering and the result was presented at FOCS, which is one of the two top conferences of theoretical computer science. Ailon and Charikar wrote “Determining whether a constant approximation can be obtained is a fascinating question”, and indeed this is exactly what is achieved.

The new constant factor approximation result has been accepted for the 62^nd Annual IEEE Conference on Foundations of Computer Science to be held in Colorado. This is one of two top annual conferences of Theoretical Computer Science. A free version is found here.