Milling Machines and Disks in Curves of Bounded Convex Curvature

Mikkel Abrahamsen explains the result of the paper: Disks in Curves of Bounded Convex Curvature by Anders Aamand, Mikkel Abrahamsen, and Mikkel Thorup. The paper can be found here.

Figure 1: Left: A milling machine. The model is the Rabbit Mill v3.0 from SourceRabbit, who kindly provided permission to use the picture. Right: A milling tool. The machine rotates the tool at high speed and makes the center of the tool follow the toolpath. The sharp teeth of the tool then cuts away all material within some distance from the toolpath. Picture by Rocketmagnet, licensed under CC BY-SA 3.0.

Milling machines (Figure 1) are used to cut out the inside of a closed curve, and these curves form an interesting generalization of a kind of curves classically studied by mathematicians. They have studied curves of bounded curvature, which are curves that cannot turn too sharply in any direction. However, milling machines can handle sharp corners into the inside of the curve, but not sharp corners into the outside (Figure 2).

Figure 2: Here the tool is the dashed circle, and we try to cut out the heart-shaped region. We can remove the dashed region, but not the remaining part of the heart close to the bottom corner. However, the top corner is no problem. The fundamental difference is that the bottom corner is convex whereas the top corner is concave. This explains why it is natural to consider curves with curvature restricted in just one direction.

This leads to curves of bounded convex curvature (but unbounded concave curvature). Mathematically speaking, the bound on the convex curvature is defined in terms of a unit disk: the curve can never turn sharper towards its own interior than a unit disk (Figure 3). Our contribution is a proof that the interior of any simple, closed curve of bounded convex curvature contains an open unit disk.

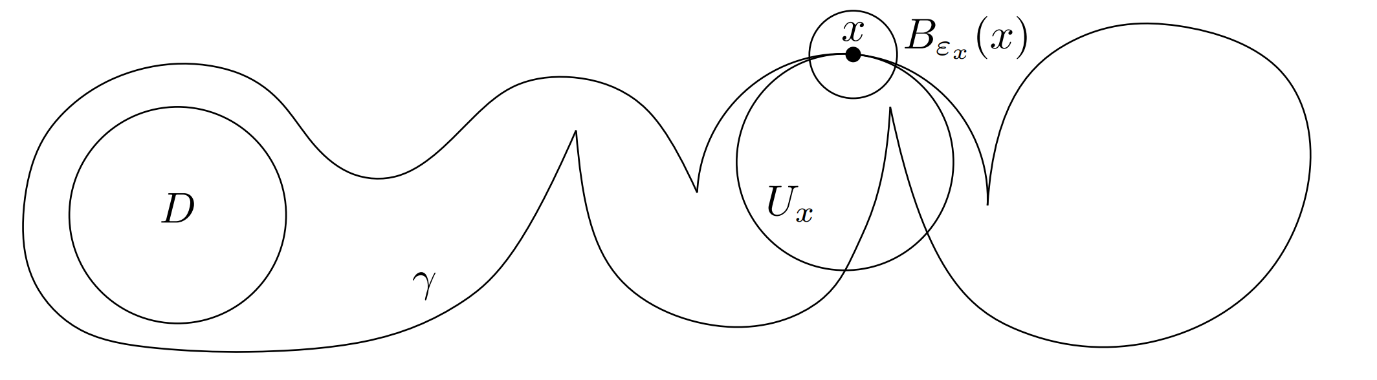
Figure 3: A curve γ with bounded convex curvature: at any point x on γ, there is a unit disk U_x with x on the boundary such that the interior of U_x is contained in the interior of γ close to x. We prove that the interior of such a curve always contains an open unit disk D.

In addition to being more general, our new definition also has the advantage that it is simpler to understand, since it does not rely on a parametrization of the curve. Instead, it is defined directly from the geometry of the curve.

The new theorem is needed for an algorithm that is guaranteed to find the maximal area a milling machine can cut out from the inside of a given closed curve [Abrahamsen and Thorup, Symposium on Computational Geometry 2016, https://arxiv.org/abs/1603.02080]. Factories want to cut out as much as possible with a given milling tool, since the remaining part has to be cut out with finer tools that are more expensive to use. The milling machines often produce a large number of identical objects. There is therefore a lot to save if we in advance compute the best use of each milling tool involved in the process.