Hashing for Strong Concentration

Hash functions are a fundamental and very commonly used tool for statistical analysis of large amounts of data. To understand what a hash function is, it is helpful to think of how it can help you tidy up your workshop. Imagine that you own a big collection of tools that you want to put into the drawers of your workshop. The drawers may have limited capacity, so you want a relatively even distribution of the tolls. Moreover, you want to quickly be able to find your tools when you need them. The idea behind hashing is having a function decide where you put the tools. For instance, when you need the hammer, you calculate the function to figure out which drawer to look into. If you do indeed own a hammer, you can quickly look through that drawer and find it. And if it’s not there, you conclude that you don’t own a hammer not having to look through any of the other drawers. This example may seem a bit silly but in the analogue with data analysis, the tools correspond to data, and real world data sets often consists of millions of data points which makes it a non-trivial task to store them efficiently.

How do we choose the hash function? Real world data nearly always have hidden structures, so if we just choose some function, it could potentially give a bad distribution of the data. For example, if you partitioned your tools according to first letter, you would quickly realise that some drawers end up completely empty, while others get overfull (screws, screwdriver, spanner, scissors, spirit level). A first idea for solving this problem is to choose a random function. A random function will not ‘care’ about hidden structures, and it is likely to give nice distributional properties of the data. Unfortunately, it is impossible to implement a fully random function. The solution is to choose the function in between: On the one hand it has to be concrete enough to be easily described and calculated. On the other hand, it has to have enough randomness to distribute data nicely.

Today, hashing is far from restricted to this classic application. In fact, hashing is used in nearly all analyses of the statistics of big data. The study of fast and reliable hashing is therefore an important area where breakthroughs can have major practical impact. The mathematically challenging task is always to prove that regardless of the input data, the hashing based algorithm will provide good statistical estimates high probability.

In our recent STOC paper by Anders Aamand, Jakob B. T. Knudsen, Mathias B. T. Knudsen, Peter M. R. Rasmussen, Mikkel Thorup, we present a practical and very fast family of hash functions, tabulation-permutation hashing, and prove that it satisfies a fundamental and important statistical property. This property relates to the normal distribution, that is, the classical bell curve (see the figure). Most of the probability mass of the normal distribution is concentrated within a few standard deviations of the mean, and going further out, the bell curve fades extremely quickly, in fact faster than exponentially. Essentially, this concentration is what allows for good statistical estimates based on sampling. As an example, think of an election poll, where we can use the opinions of a relatively small random sample of the voters to predict the final distribution of all the votes with good accuracy. The point is that the fraction of people from a random sample voting for party X will closely follows a normal distribution. Since the normal distribution is tightly concentrated around its mean, this fraction will be a good estimator for the fraction of people from the entire population voting for party X.

Large-scale data, e.g., Internet traffic data often arrives as data streams. These streams are so huge and passes by so fast, that we only get very limited time to look at the data. If we’re not done in time, the information is lost. To analyse these streams, we can apply a similar approach to the one described above. We sample a smaller subset of the stream, perform the analysis on this smaller subset, and finally scale the results to make statistical conclusions for the whole stream. Here it is important that the sampled subset of the stream represents the entire stream, so that the scaling is unlikely to produce big errors. If the subset of the stream is sampled using a fully random hash function, we will have the nice resemblance with the normal distribution as described above, and we can thus obtain good statistical estimators. But again, fully random hash functions cannot be used in practice!

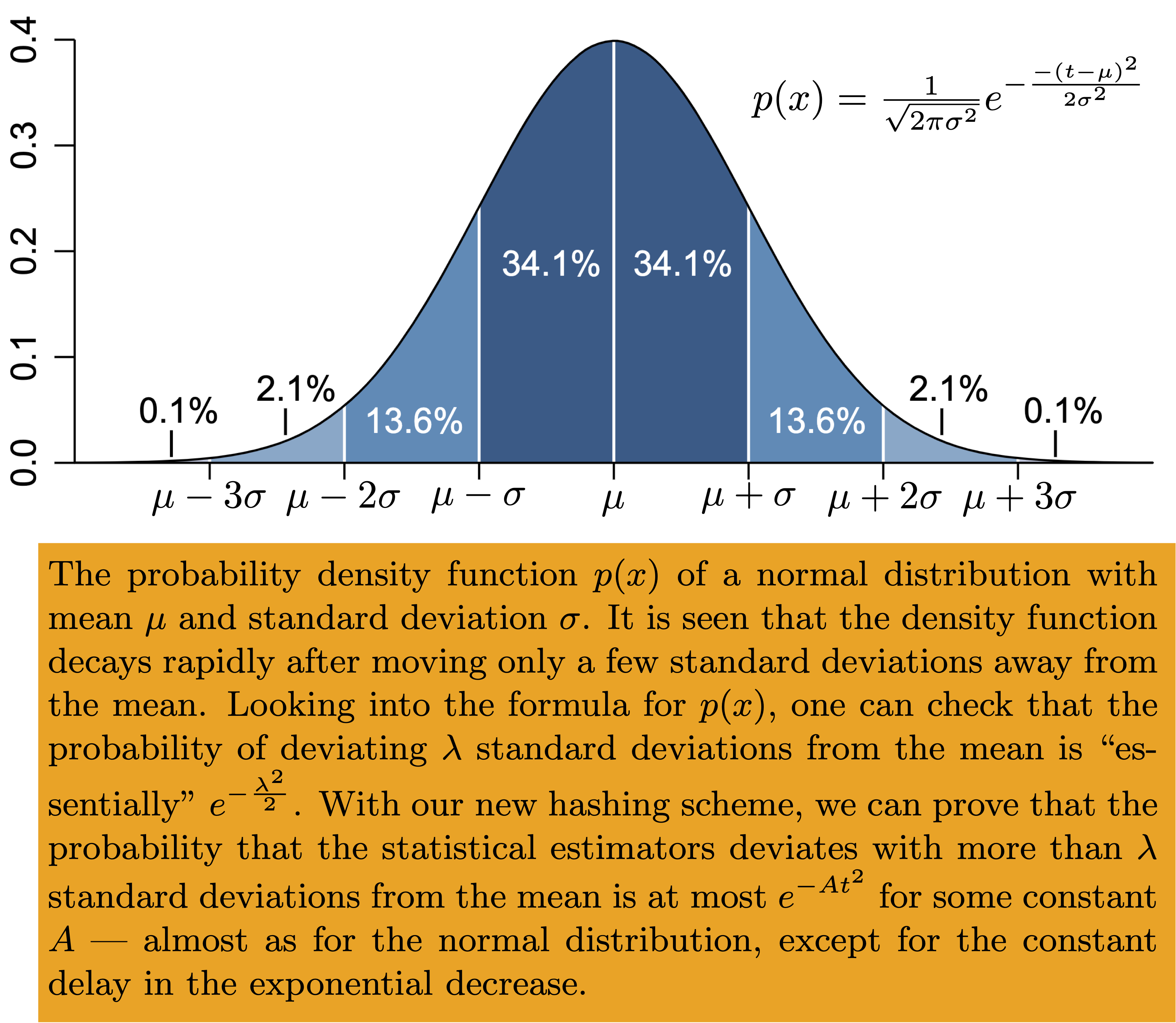
With this result, we show that when using our hashing scheme, we do obtain the same good theoretical guarantees as if we had used a fully random hash function — the bell curve again shows up! Our hashing scheme is the first known practical hash function with this property and our experiments show that its speed is comparable to some of the fastest hash functions in use in practice (which have no similar theoretical guarantees) and around 100 times faster than previously known schemes with similar theoretical guarantees. This means that the above presented algorithms for statistical analysis can now be implemented in a very fast and efficient way. And moreover, we know with mathematical certainty that the algorithms are likely to produce good estimators.

In other words, we no longer have to settle with a too weak hash function, crossing our fingers and hoping for the best!