BARC has 3 accepted papers at STOC ’18
Yet again, DIKU’s research centre BARC has papers accepted at a prestigious conference. This time at the STOC 2018, which will be held on 25-29 June 2018 in Los Angeles.
At the 50th ACM Symposium on Theory of Computing (STOC 2018), a number of BARC researchers will present their works.
The three accepted papers
Fast Fencing
Authors: Mikkel Abrahamsen, Anna Adamaszek, Karl Bringmann, Vincent Cohen-Addad, Mehran Mehr, Eva Rotenberg, Alan Roytman, and Mikkel Thorup.
Unit circles in the plane can be “fenced in” by closed curves called “fences”, as in this picture, where 11 circles are fenced in by 3 curves. The natural computational question is to find a set of fences for a given set of circles, given by their midpoints, with as little total fence length as possible. It is clear that this question boils down to deciding which points end up in same same fence, and that a priori the number of possibilities is exponential in the number of points. The new result is an algorithm with polynomial running time.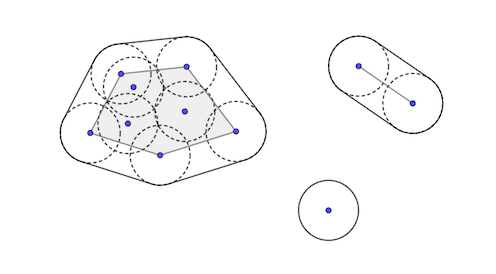
The Art Gallery Problem is ∃R-complete
Authors: Mikkel Abrahamsen, Anna Adamaszek and Tillmann Miltzow
The art gallery problem is a famous problem in computational geometry, determining how many guards are needed to “see” all walls in an idealised, polygonal art gallery. The article shows that the problem is complete for the complexity class known as “Existential Theory of the Reals”. This means that the art gallery problem is as difficult as determining whether a given polynomial in many variable and integer coefficients has a real root. To establish the result, a given polynomial is transformed into an art gallery, where the guards play the roles of the polynomial’s variables. Addition and multiplication of variables then corresponds to placement of guards in specially constructed wings in the art gallery. The figure shows a wing that simulates addition.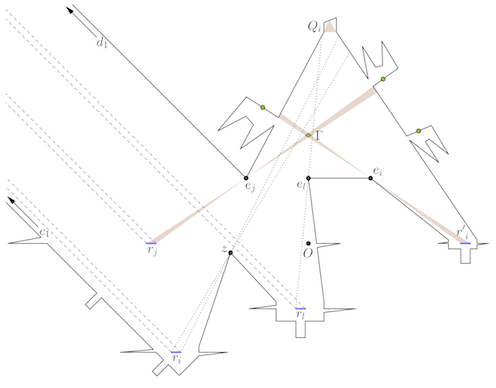
Extensor-coding
Authors: Cornelius Brand, Holger Dell and Thore Husfeldt
For given integer k, the k-path problem is to detect occurrences of a path of length k in a given graph. This is known to be a problem whose complexity grows exponentially with k. The new result is that the number of such paths can be approximately counted in time 4^k by a randomised algorithm. Of particular interest is the technique: the algorithm translates the combinatorial problem into an expression in the “Exterior algebra” of Grassman, and performs all computation in that algebra. The cancellation rules of the “exterior product” unify and simplify a number of previous approaches for this problem.
